Operacions amb fraccions (I). Comú denominador. Suma i diferència

Comú denominador

La suma i la diferència de fraccions són dues operacions que exigeixen que els denominadors siguen iguals per resoldre-les, ja que no és possible sumar desens amb quarts o cinquens ni tampoc no ho és restar-los.

Allò que cal fer és passar a comú denominador, mitjançant l'eina ja apresa del mínim comú múltiple (mcm) dels denominadors per a construir fraccions equivalents amb idènntic denominador.

Una vegada hem obtingut el mínim comú múltiple dels denominadors, cal utilitzar-lo com a denominador de les fraccions equivalents, on posarem com a numerador el resultat de multiplicar el numerador original i el mínim comú multiple, que estarà dividit pel denominador original.

Exercici 8. Passa a comú denominador els següents parells de fraccions:

• 3/6, 1/12
• 5/10, 1/5
• 5/25, 25/100
• 25/12, 3/5
• 18/3, 6/5

Solució:

• 3/6, 1/12: 6/12, 1/12
• 5/10, 1/5: 5/10, 2/10
• 5/25, 25/100: 20/100, 25/100
• 25/12, 3/5: 125/60, 36/60
• 18/3, 6/5: 90/15, 18/15

Suma de fraccions

Com ja hem esmentat, és necessari que els components de la suma tinguen el mateix denominador. Si no ho són, hem de passar-los a comú denominador i obtindre fraccions equivalents que tinguen idèntic denominador (mcm) de la manera que ja s'ha explicat amb anterioritat, i posarem com a numerador el numerador original però multiplicat pel mínim comú múltiple (mcm) i dividit pel denominador original.

Posteriorment, obtindrem el resultat sumant els numeradors deixant com a denominador el mínim comú múltiple (mcm).

Suma de fraccions

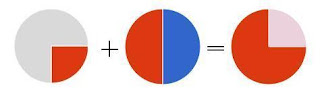Suma de fraccions, gràficament

Exercici 9. Suma les següents fraccions com s'ha explicat:

• 3/6 + 1/12
• 5/10 + 1/5
• 5/25 + 25/100
• 25/12 + 3/5
• 18/3 + 6/5

Solució:

• 3/6 + 1/12 = 6/12 + 1/12 = 7/12
• 5/10 + 1/5 = 5/10 + 2/10 = 7/10
• 5/25 +25/100 = 20/100 + 25/100 = 45/100
• 25/12 + 3/5 = 125/60 + 36/60 = 161/60
• 18/3 + 6/5 = 90/15 + 18/15 = 108/15

Diferència de fraccions

Com que la diferència (o resta) és l'operació inversa de la suma, el procés per a calcular-la és exactament el mateix que el de la suma; és a dir, les fraccions han de tindre denominador comú. En cas contrari, haurem d'obtindre'l mitjançant el mínim comú múltiple per a trobar fraccions equivalents.

El resultat tindrà com a numerador la diferència dels numeradors i com a denominador el mínim comú múltiple (mcm).

Diferència de fraccions

Diferència de fraccions, gràficament

Exercici 10. Resta les següents fraccions com s'ha explicat:

• 3/6 - 1/12
• 1/5 - 5/100
• 5/25 - 25/100
• 25/12 - 3/5
• 4/5 - 10/13

Solució:

• 3/6 - 1/12 = 6/12 - 1/12 = 5/12
• 1/5 - 5/100 = 20/100 - 5/100 = 15/10
• 5/25 - 25/100 = 20/100 - 25/100 = -5/100
• 25/12 - 3/5 = 125/60 - 36/60 = 89/60
• 4/5 - 10/13 = 52/65 + 50/65 = 2/65

Important 1

Després d'operar amb les fraccions, és convenient que simplifiquem fins que trobem la fracció irreductible del resultat, sempre que això siga possible.


Exercici 11. Resol les següents operacions amb fraccions i simplifica al màxim:

• 3/4 + 1/3 - 1/4
• 6/5 + 5/6 -1/2
• 25/3 + 3/10 - 1/30 + 2/30

 Solució:

• 3/4 + 1/3 - 1/4 = 9/12 + 4/12 - 3/12 = 10/12 = 5/6
• 6/5 + 5/6 -1/2 = 36/30 - 25/30 + 15/30 = 13/15
• 25/3 + 3/10 - 1/30 + 2/30 = 250/30 + 9/30 - 1/30 + 2/30 = 260/30 = 26/3

 

Important 2

En la pàgina Vídeos d'aquest bloc, trobareu el Vídeo 2, amb una Pechakucha sobre aquesta entrada.